Жабко А.П. Сборник задачи и упражнений по теории управления:
стабилизация программных движений: Учебное пособие / А.П. Жабко,
А.В. Прасолов, В.Л. Харитонов. Москва: Высшая школа, 2003.
№ 52. Восстановить по наблюдению начальное состояние системы
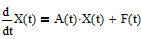 (1)
(1)
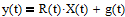 ,
, 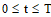 (2)
(2)
Результаты наблюдения на промежутке [0,T]:
I. Фундаментальная матрица системы  :
:
II. Исследование системы (1)-(2) на полную наблюдаемость.
Матрица Грама для системы функций, еоторые являются столбцами матрицы H(t):
Вывод. Так как матрица Грама является невырожденной, то столбцы матрицы H(t) линейно независимы на отрезке [0,T].
III. Восстановление начального состояния.
IV. Состояние системы на промежтке [0,T] определяет функция:
Полученное выражение совпадает с выражением, описывающим результаты наблюдения:
Фазовая траектория уравнения (1), соответствующая начальному условию:
Исследование на полную наблюдаемость и восстановление начального состояния с помощью матрицы N(t) из достаточного условия полной наблюдаемости
Если выбрать другое значение для момента времени 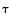 :
:
Результат восстановления не изменился: