Наблюдаемость линейной системы:
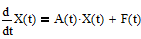(1)
, 
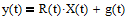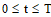(2)
Жабко А.П. Сборник задачи и упражнений по теории управления:
стабилизация программных движений: Учебное пособие / А.П. Жабко,
А.В. Прасолов, В.Л. Харитонов. Москва: Высшая школа, 2003.
I. Фундаментальная матрица системы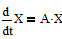 
:
II. Исследование системы (1)-(2) на полную наблюдаемость.
Матрица Грама для системы функций, которые являются столбцами матрицы H(t):
Вывод. Так как матрица Грама при любом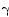 
является вырожденной, то столбцы матрицы H(t) линейно зависимы на отрезке [0,T]. Следовательно, при любом значении параметра 
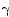система не является полностью наблюдаемой.
Дополнение. Исследование системы (1)-(2) на полную наблюдаемость.
Матрица Грама для системы функций, которые являются столбцами матрицы H(t):
Выясним, при каких определитель равен 0:
Вывод. Следовательно, если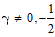 
, то система будет полностью наблюдаемой.
