Жабко А.П. Сборник задачи и упражнений по теории управления:
стабилизация программных движений: Учебное пособие / А.П. Жабко,
А.В. Прасолов, В.Л. Харитонов. Москва: Высшая школа, 2003.
№ 65.
Для управляемой системы
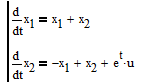(1)
построить программное управление для перевода системы из состояния
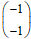в состояние 
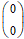на промежутке времени [0,4π]
Фундаментальная матрица системы 
:
Так как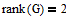 
, то пара 
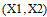управляема на промежутке [0,4π].
Построим программное управление в виде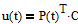 
, где С - постоянный вектор,
подлежащий определению. Вектор C является решением уравнения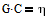 
, где:
и программное управление:
Определим программное движение, как решение задачи Коши для системы (1) с начальным условием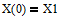 
:
