Задача 6. 1). Восстановить текущее состояние системы:
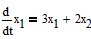
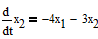
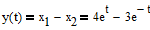
Исследуем столбцы матрицы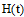 
на линейную независимость.
Построим матрицу Грама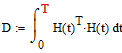 
для системы функций, которые являются столбцами матрицы 
:
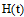Вычислим определитель матрицы Грама:
Выясним, при каких T он обращается в ноль:
Так как определитель отличен от нуля при любых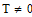 
, то столбцы матрицы 
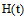линейно независимы на любом промежутке [0, T], и, следовательно, система полностью наблюдаема на любом промежутке [0, T].
Восстановим начальное состояние.
При этом текущее состояние определим по формуле: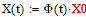 
Исследование на полную наблюдаемость с помомощью критерия Калмана
Заданная система полностью наблюдаема на любом промежутке времени.
Восстановление текущего состояния с помощью матрицы наблюдаемости
Результат восстановления не изменится, если выбрать другой момент времени
